K-Nearest Neighbors（K最近邻）

KNN算法是一种简单的机器学习算法，用于分类和回归问题。KNN算法的基本思想是找到与给定数据点最相似的K个数据点，然后将这些数据点的标签进行投票，以确定给定数据点的标签。 KNN算法的优点是简单易用，不需要训练过程，只需要存储训练数据。缺点是计算复杂度高，需要遍历整个训练数据集。 KNN算法的实现步骤如下：

计算训练数据集中每个数据点的距离：使用欧氏距离、曼哈顿距离等方法计算训练数据集中每个数据点的距离。
选择K个最相似的数据点：根据距离排序，选择距离最小的K个数据点。
确定给定数据点的标签：对K个最相似的数据点的标签进行投票，选择出现次数最多的标签作为给定数据点的标签。

应用

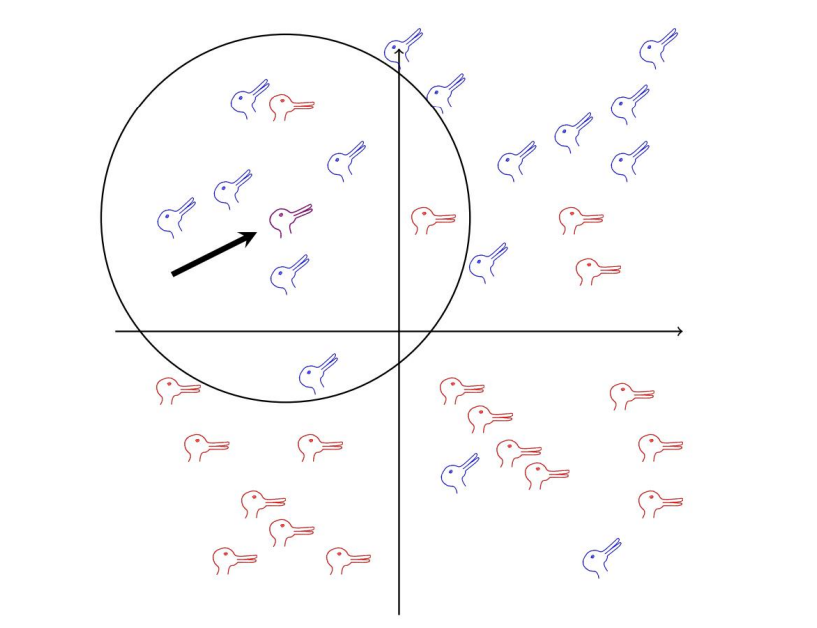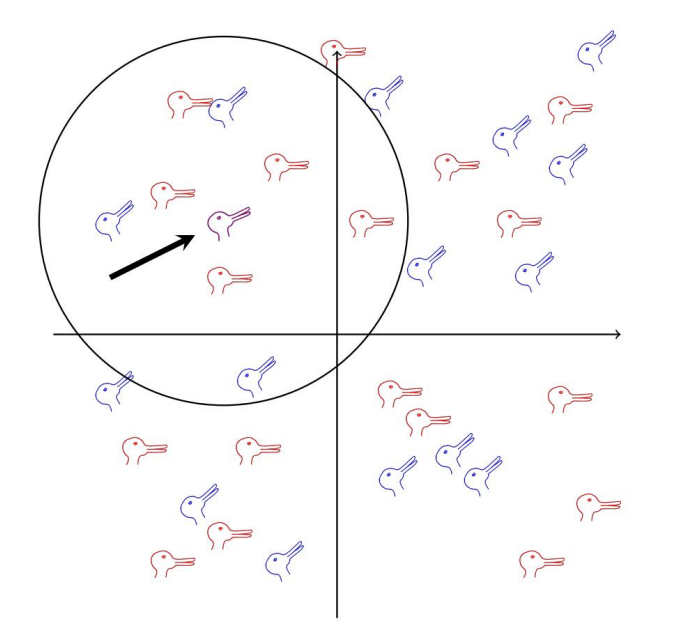program 鸭⼦和兔⼦代表标记数据，⿊⾊箭头指向未标记的数据点。这⾥，k = 8，圆圈内的点中有六个是兔⼦，因此未标记的点将被标记为兔⼦。 program 在这种情况下，未标记的点将被标记为鸭⼦，但从数据点的混合来看，不清楚这是否有⽤，每个点的位置与其标签关系不⼤。这个问题是⼀个表⽰问题，数据点由坐标表⽰，但这些坐标可能⽆法以有⽤的⽅式表⽰标签。在许多算法中，部分计算与寻找良好的表⽰有关，这可能涉及原始坐标的映射。

该⽅法并不详细地依赖距离，它只⽤它来计算接近度。事实上，即使数据空间没有坐标，但有计算距离的⽅法，例如时间序列，你也可以期望该⽅法能很好地⼯作。

相反，k-nn 的⼀个优点是它不假设位置以任何特定的⽅式代表标签，它只是假设带有特定标签的点可能靠近带有该标签的其他点，此⽰例显⽰的数据中鸭⼦和兔⼦之间的分界线不在⼀条线上

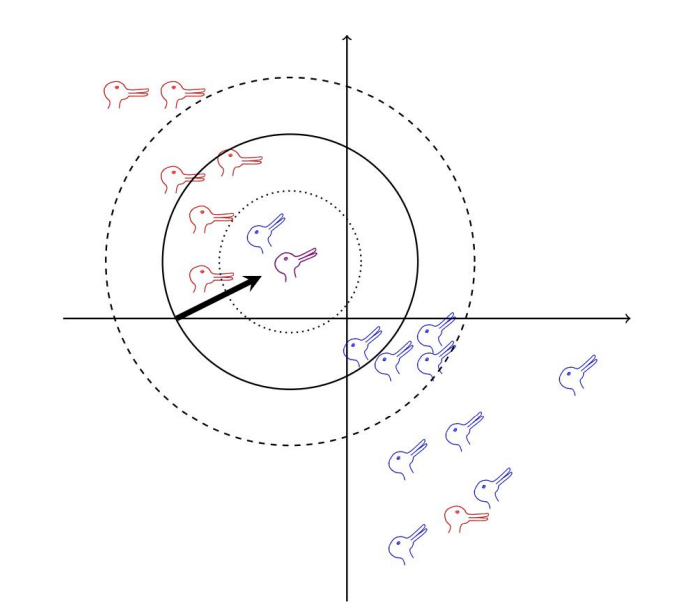program 关于K值的选择问题！这⾥，很明显有⼀个兔⼦簇和⼀个鸭⼦簇；兔⼦簇中有⼀只鸭⼦，鸭⼦簇中有⼀只兔⼦；这表⽰可能存在错误标记或其他噪⾳。现在，如果 k = 5，对应于具有实线边界的圆，则未标记的点被标记为鸭⼦，这可能是正确的；如果 k = 1，则 k 值更容易受到噪⾳的影响，实际上，这⾥会导致未标记的点被标记为兔⼦，同样，如果 k = 9，对应于虚线圆，邻域⼤于标签的聚类结构，同样，未标记的点将被标记为兔⼦。

K值的选择方法

一般经验

通常K值选择为一个较小的奇数（避免分类时出现平票情况）。
一般K为N的开方，其中n是训练样本总数！

交叉验证

交叉验证是KNN算法的一个重要参数选择方法，通过交叉验证来选择最佳的K值。
交叉验证的思路是，将数据集划分为训练集和测试集，然后对训练集进行KNN算法的训练，对测试集进行预测，并计算预测准确率。

网格搜索

给出合理范围（如K=1到K=20）对每一个K值训练并评估模型，现在表现最优的K

from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
import numpy as np

# 示例数据（自行替换为实际数据）
X = [[1, 2], [2, 3], [3, 4], [5, 6], [6, 7]]  # 特征
y = [0, 0, 1, 1, 1]  # 标签

# 尝试多个 K 值
k_range = range(1, 21)
scores = []

for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    # 使用交叉验证计算得分
    score = cross_val_score(knn, X, y, cv=5, scoring='accuracy').mean()
    scores.append(score)

# 找到最佳 K 值
optimal_k = k_range[np.argmax(scores)]
print(f"最佳 K 值：{optimal_k}")

KNN算法的实现

import numpy as np
from collections import Counter
from sklearn.model_selection import KFold

# 计算欧几里得距离
def compute_distances(X_train, x_test):
    return [np.sqrt(np.sum((x_test - x_train) ** 2)) for x_train in X_train]

# KNN 分类器
def knn_classify(X_train, y_train, X_test, k):
    predictions = []
    for x in X_test:
        # 计算距离并获取最近的 k 个邻居
        distances = compute_distances(X_train, x)
        k_indices = np.argsort(distances)[:k]
        k_nearest_labels = [y_train[i] for i in k_indices]
        # 投票
        most_common = Counter(k_nearest_labels).most_common(1)[0][0]
        predictions.append(most_common)
    return predictions

# 交叉验证
def cross_validate(X, y, k_values, cv_folds=5):
    kf = KFold(n_splits=cv_folds, shuffle=True, random_state=42)
    scores = {k: [] for k in k_values}
    
    for train_index, val_index in kf.split(X):
        X_train, X_val = X[train_index], X[val_index]
        y_train, y_val = y[train_index], y[val_index]
        for k in k_values:
            predictions = knn_classify(X_train, y_train, X_val, k)
            accuracy = np.mean(predictions == y_val)
            scores[k].append(accuracy)
    
    avg_scores = {k: np.mean(scores[k]) for k in k_values}
    return avg_scores

# 网格搜索
def grid_search_knn(X, y, k_values, cv_folds=5):
    print("开始网格搜索...")
    avg_scores = cross_validate(X, y, k_values, cv_folds)
    best_k = max(avg_scores, key=avg_scores.get)
    print(f"最佳 K 值: {best_k}, 平均准确率: {avg_scores[best_k]:.4f}")
    return best_k, avg_scores

# 示例数据
if __name__ == "__main__":
    # 训练数据
    X = np.array([[1, 2], [2, 3], [3, 4], [6, 7], [7, 8]])
    y = np.array([0, 0, 1, 1, 1])

    # 测试数据
    X_test = np.array([[2, 2], [4, 5], [7, 7]])

    # 网格搜索确定最佳 K 值
    k_values = range(1, 6)
    best_k, avg_scores = grid_search_knn(X, y, k_values, cv_folds=3)

    # 用最佳 K 值预测测试数据
    predictions = knn_classify(X, y, X_test, best_k)
    print("预测结果:", predictions)

Knn 算法

K-Nearest Neighbors（K最近邻）

应用

K值的选择方法

一般经验

交叉验证

网格搜索

KNN算法的实现

CATALOG

FEATURED TAGS

FRIENDS