深度学习介绍
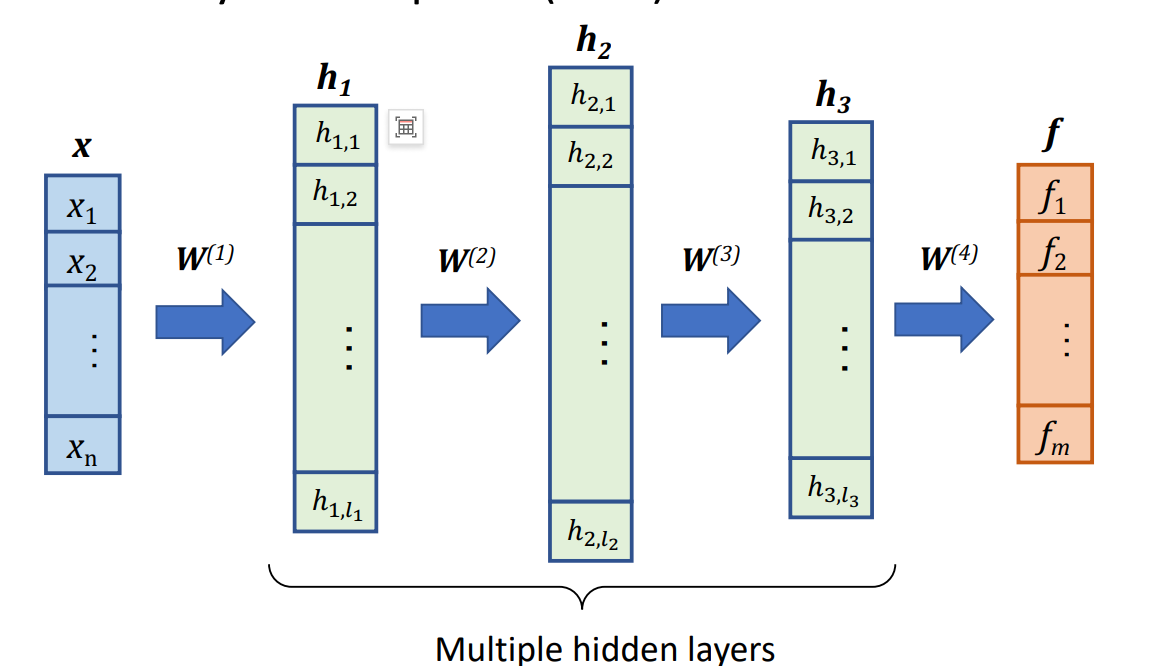✅ 多层感知机（MLP, Multi-Layer Perceptron） 是一种由多个感知器（Perceptron）组成的神经网络，通常包括一个或多个隐藏层。
✅ 深度学习（Deep Learning） 是指具有多层（多个隐藏层）神经元的神经网络，即深度神经网络（DNN, Deep Neural Networks）。
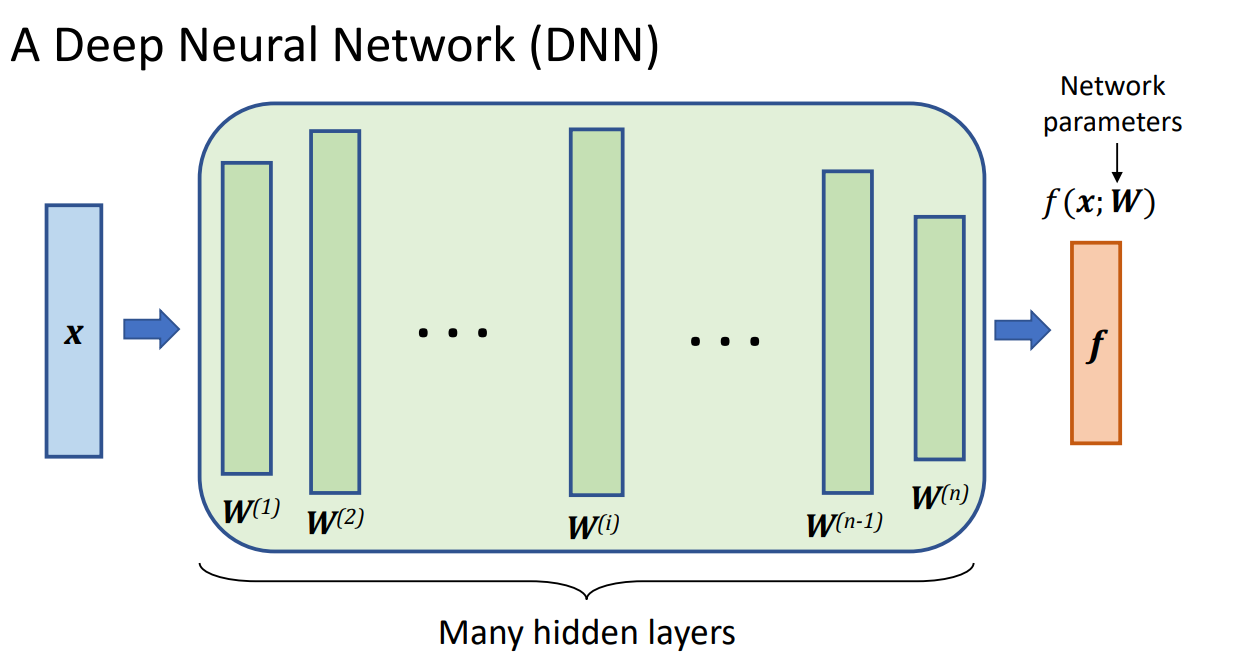
DNN可以使用不同数据类型，文本、图片、视频、录音等。
算法解析
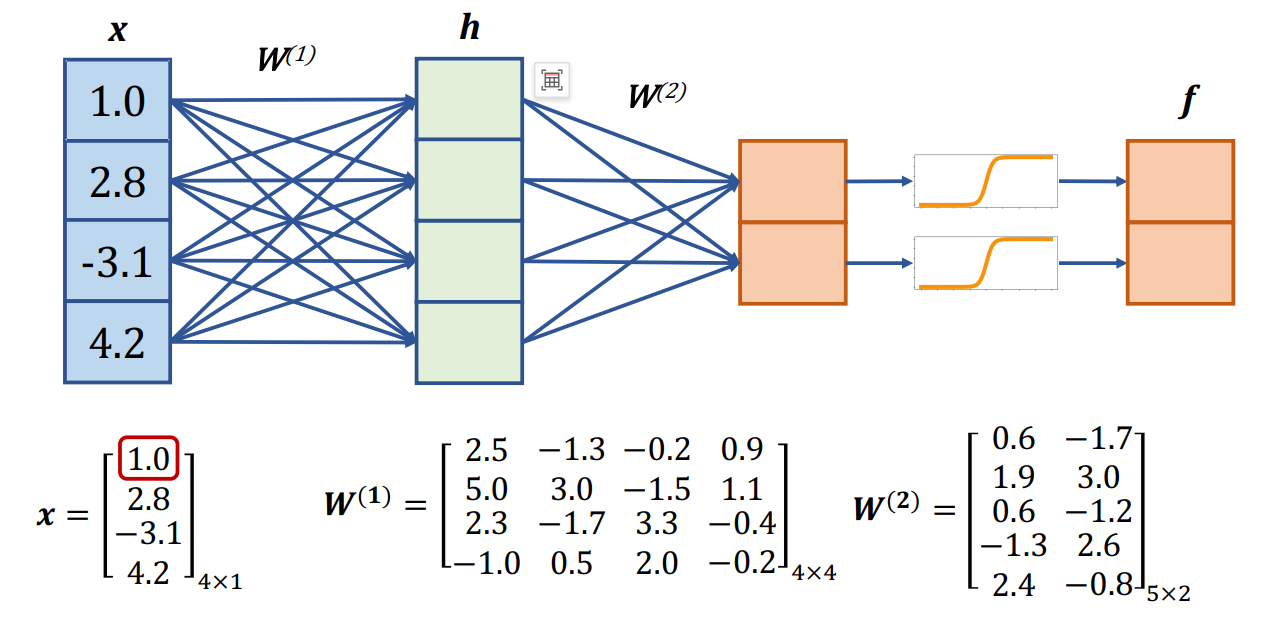
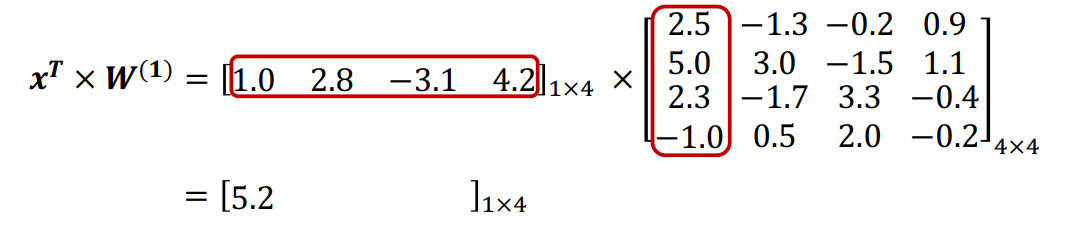
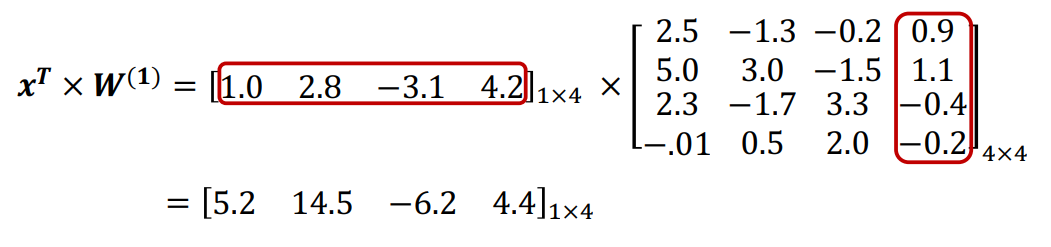
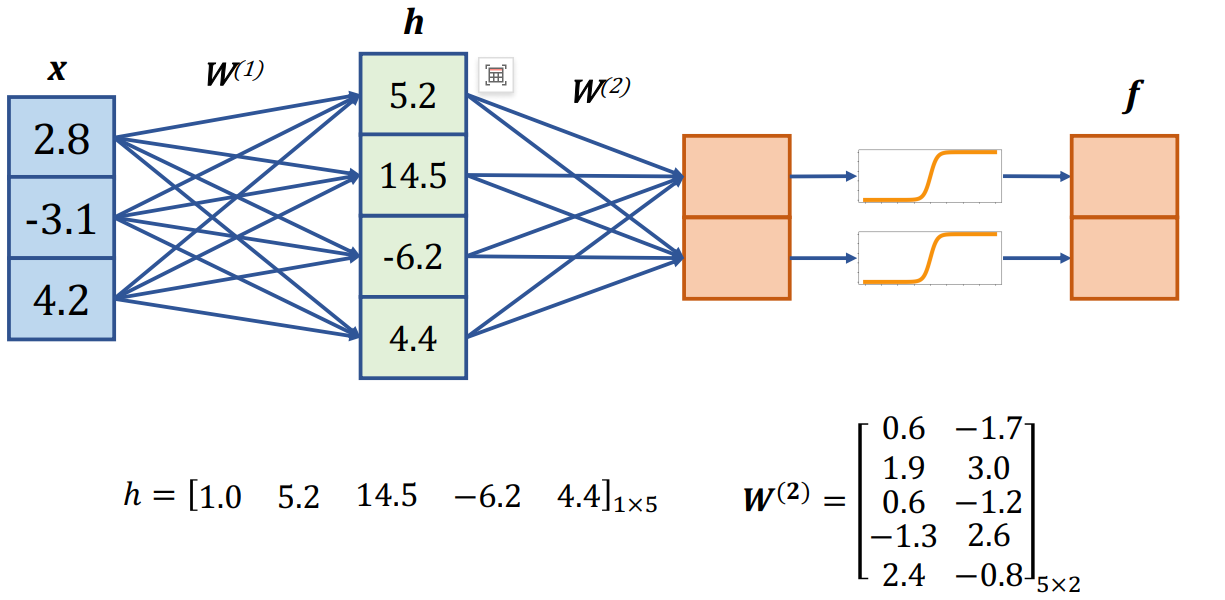
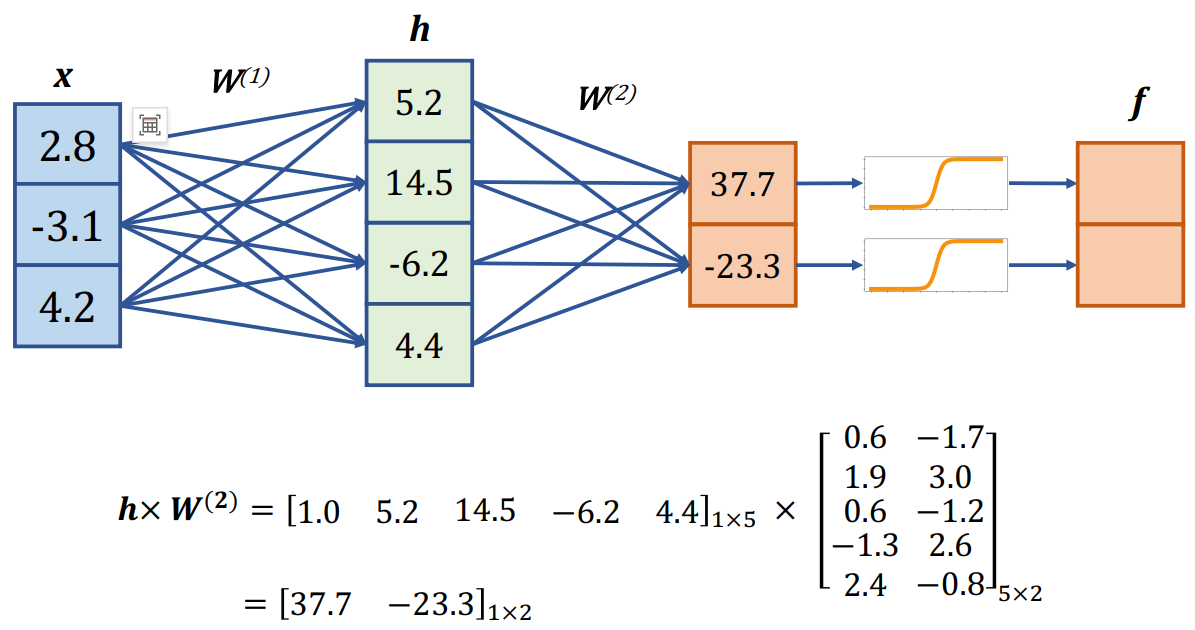
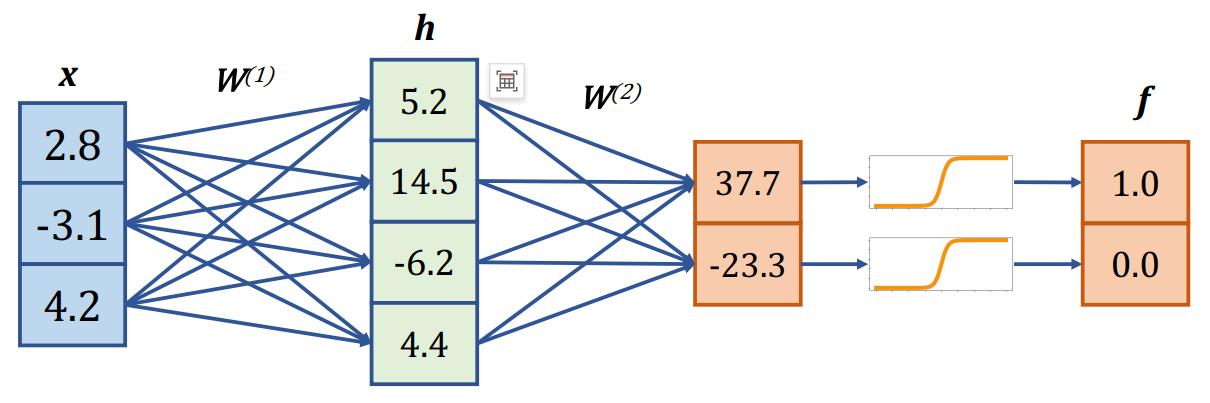
问题解决
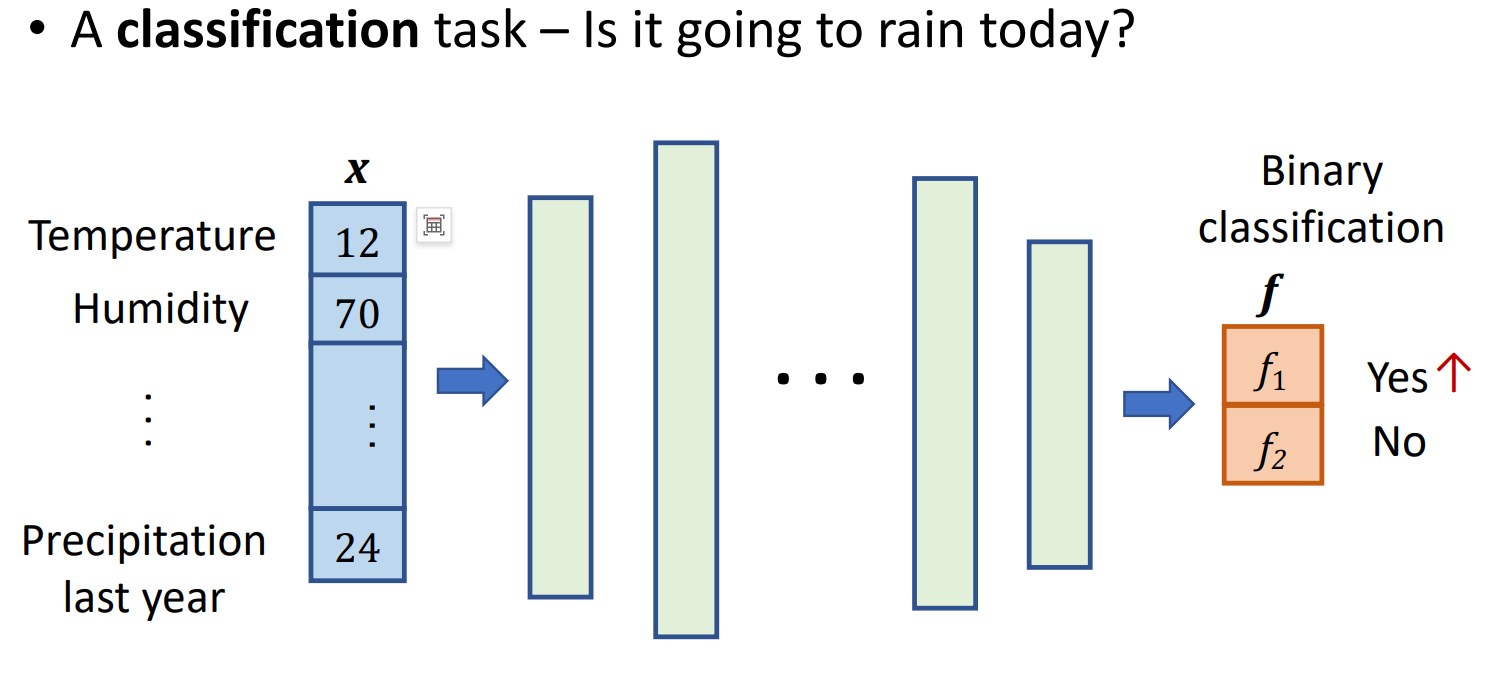
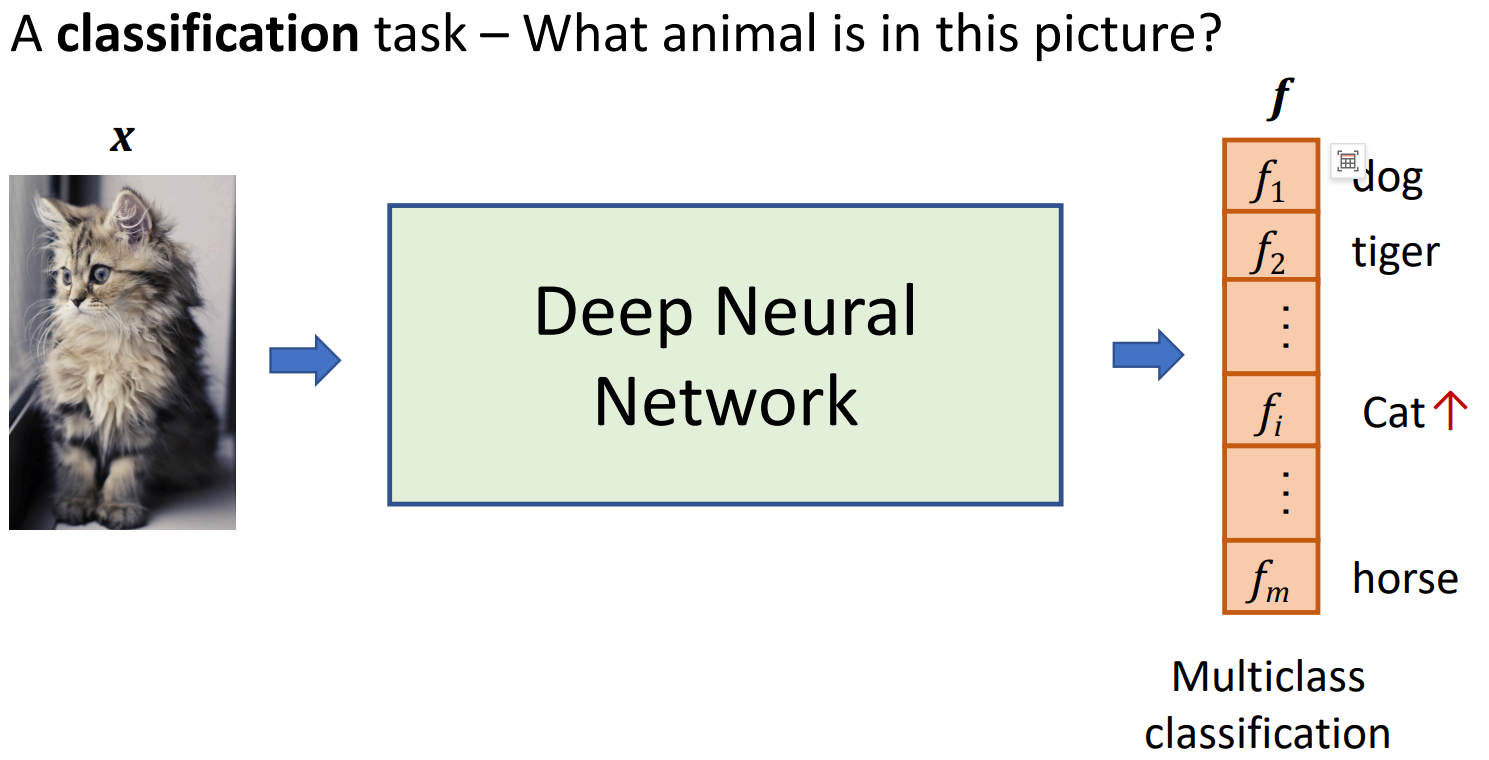
网格训练
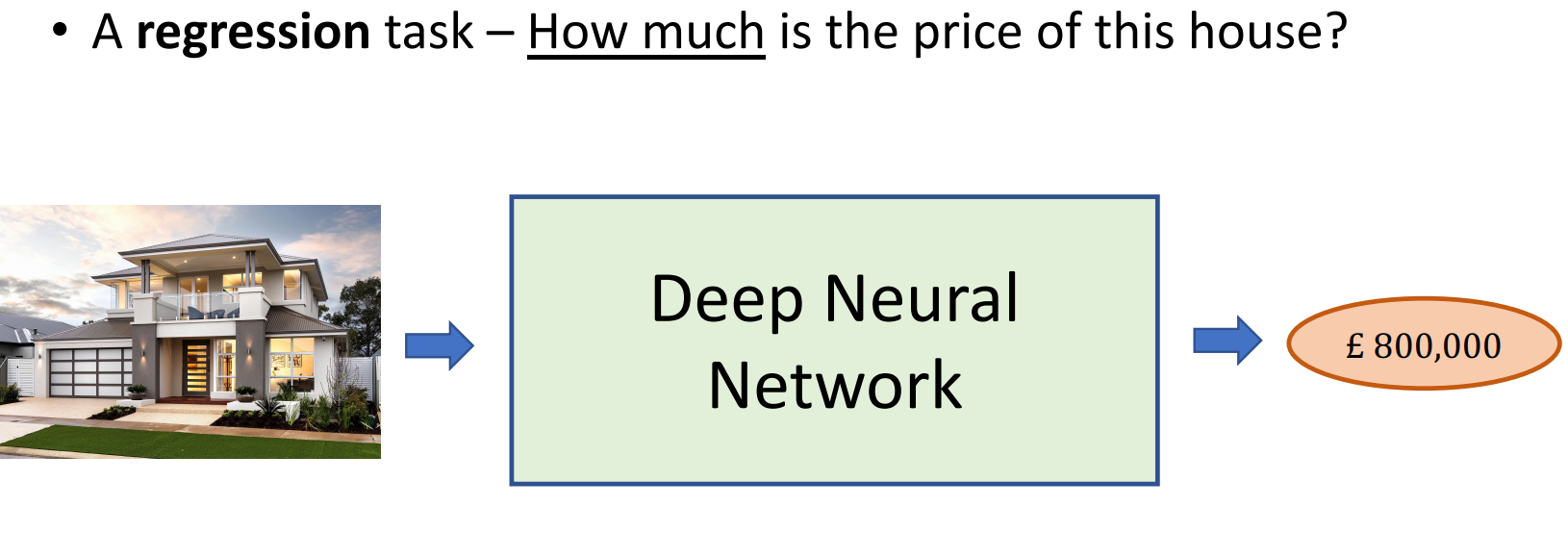
它使用当前参数集（权重）进行预测
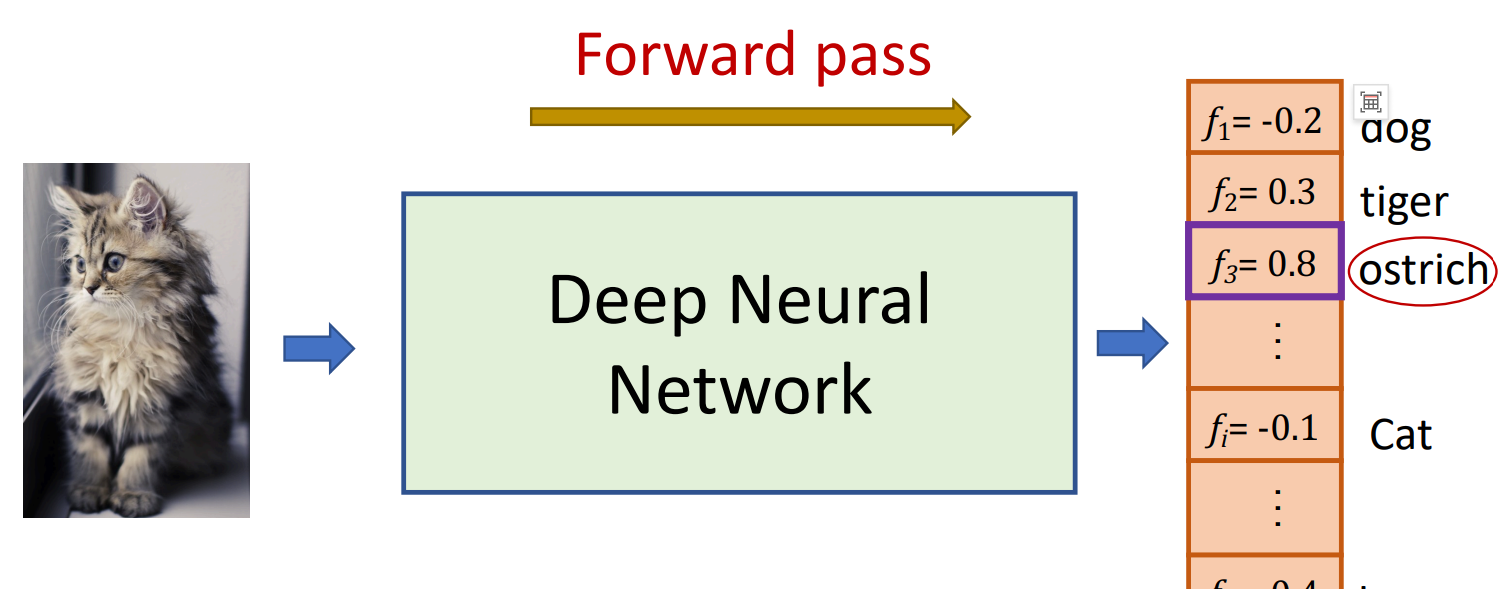我们给它一个反馈，告诉它它的预测有多好。
它根据我们的反馈更新（改进）它的参数集
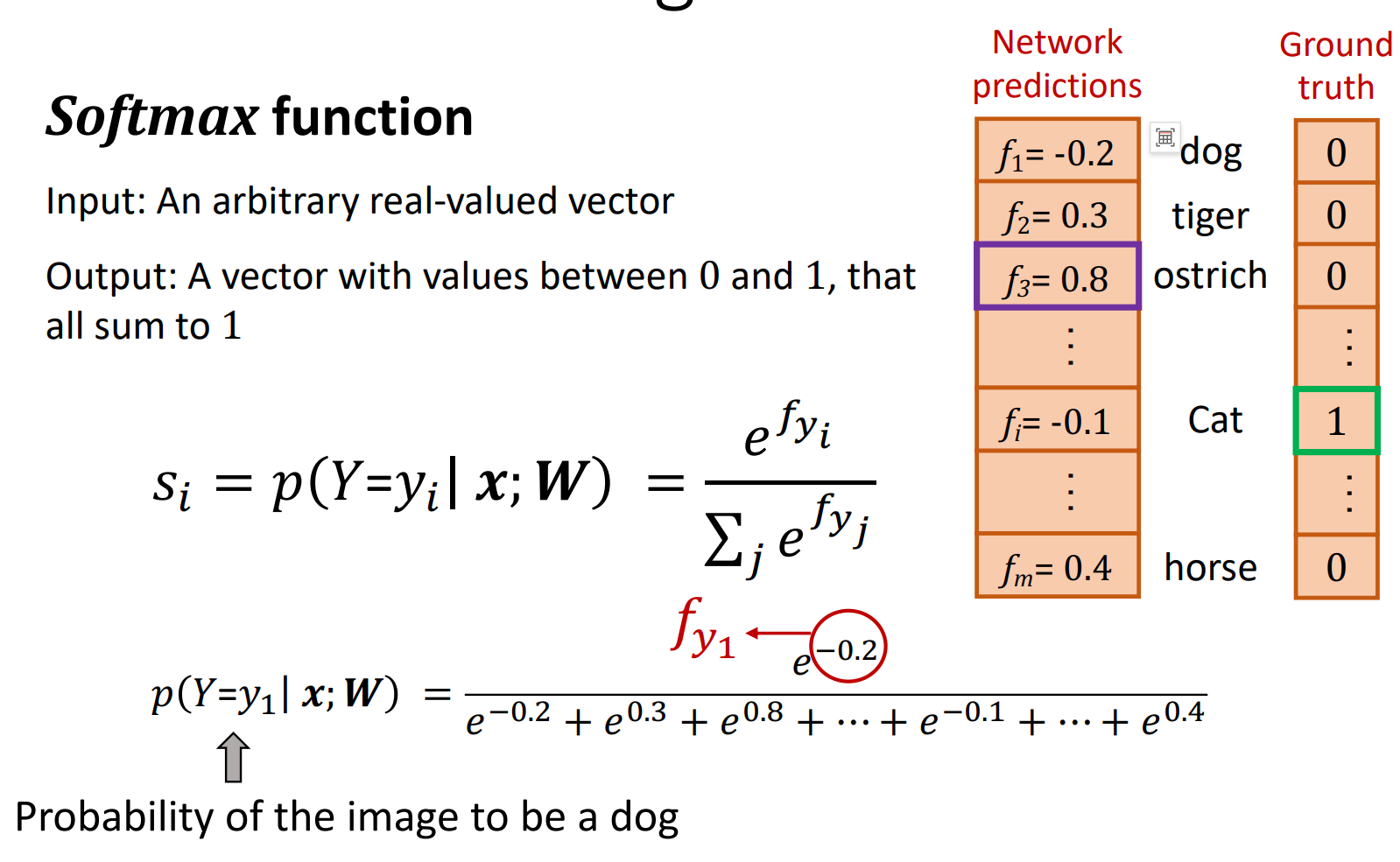
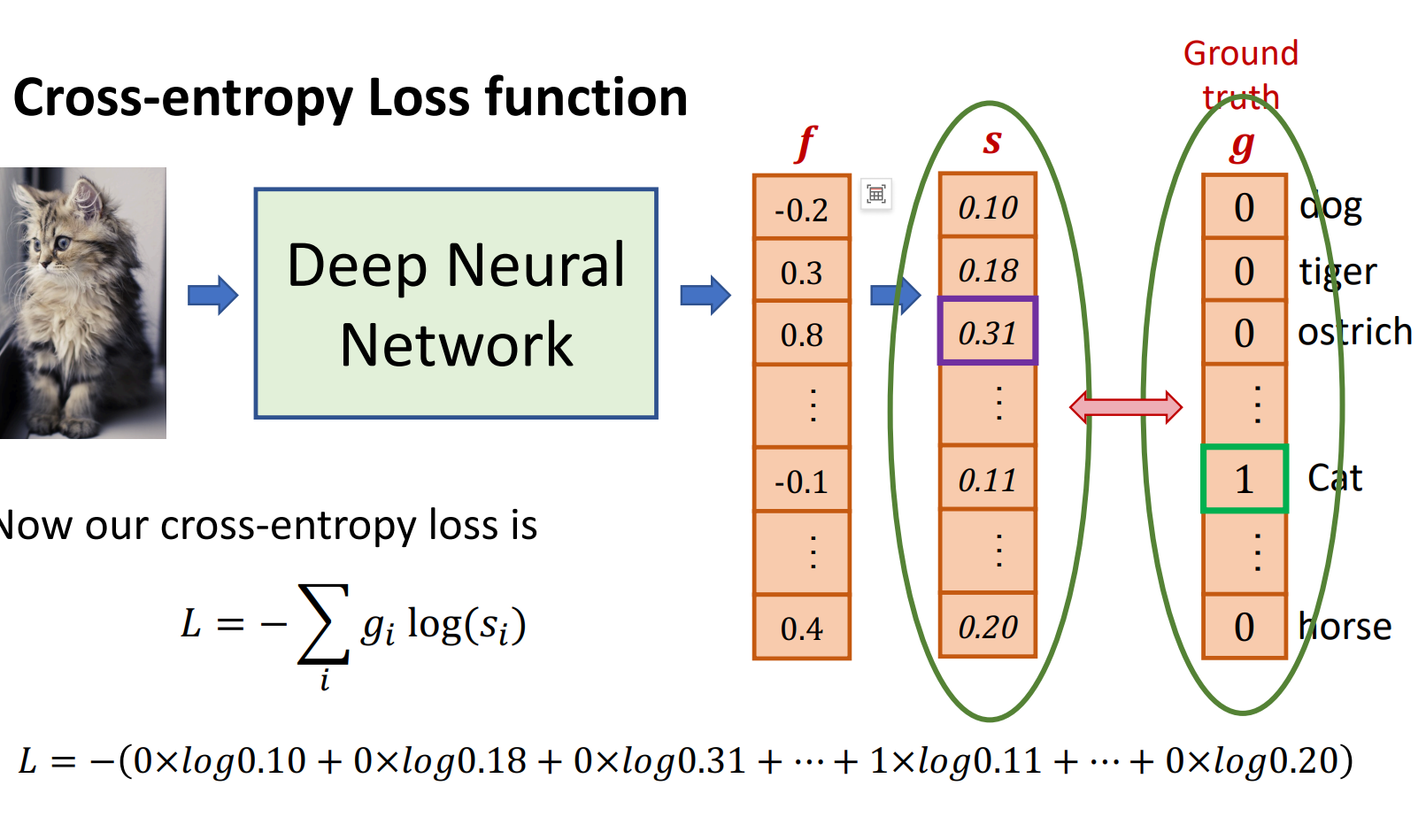
交叉熵损失函数
交叉熵损失函数（Cross-Entropy Loss Function）是深度学习中常用的损失函数。 它用于测量模型预测值与真实值之间的差异，并给出一个数值作为损失值。
交叉熵损失函数的计算公式为： $$L = - \sum_{i=1}^{n} y_i \log(\hat{y}_i)$$ 其中，$y_i$ 是真实值，$\hat{y}_i$ 是模型预测值。
它的优点是，对于多分类问题，交叉熵损失函数可以自动将预测值归一化到0到1之间，从而便于后续的优化。 它的缺点是，对于多分类问题，交叉熵损失函数无法直接给出预测值与真实值之间的差异，需要通过梯度下降法来优化。 它的优点是，对于多分类问题，交叉熵损失函数可以自动将预测值归一化到0到1之间，从而便于后续的优化。 它的缺点是，对于多分类问题，交叉熵损失函数无法直接给出预测值与真实值之间的差异，需要通过梯度下降法来优化。
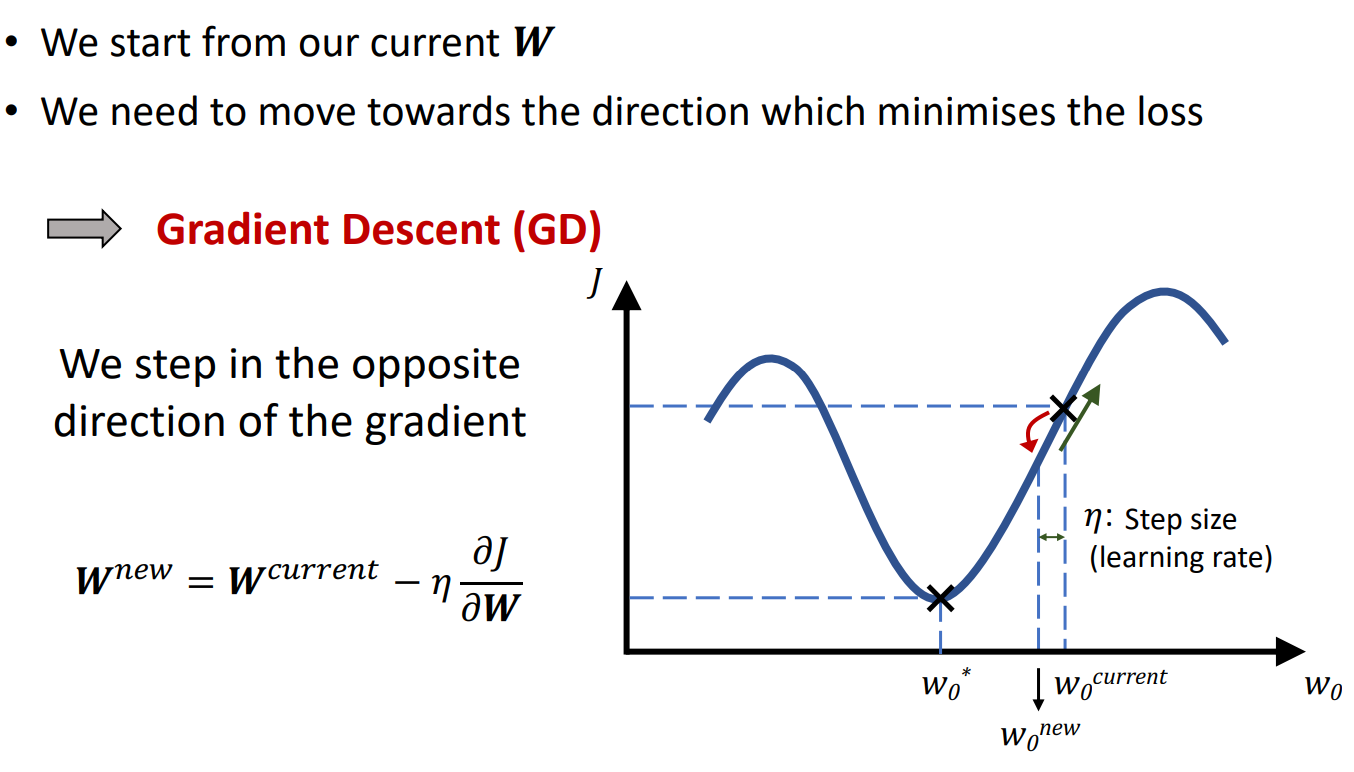
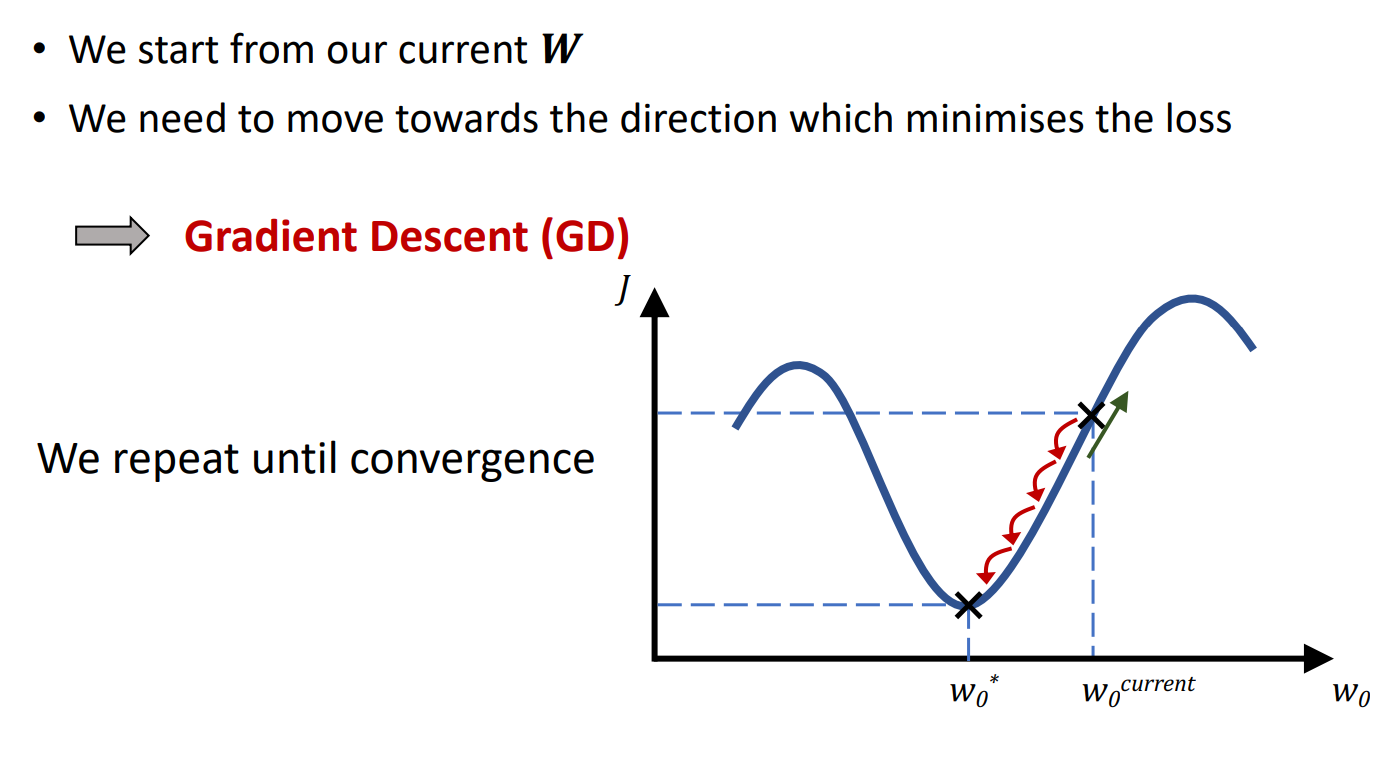
梯度下降
梯度下降（Gradient Descent）是机器学习中常用的优化算法。 它通过不断迭代更新参数，使得损失函数最小化。 在训练神经网络时，我们的目标是找到一组最优的权重（Weights, W）和偏置（Bias, b），使得损失函数 L(θ) 最小化。 但神经网络的损失函数通常是一个复杂的非线性函数，无法直接求解全局最优解，因此需要通过迭代优化的方式找到较优解，而梯度下降就是最常用的方法。 梯度下降的核心在于：
- 计算损失函数对参数的梯度（导数）。
- 沿着梯度的负方向更新参数，逐步逼近最优解。
