机器学习技术
- 监督学习:根据输入和输出数据建立预测模型;任务驱动(回归或分类);线性和逻辑回归,决策树,人工神经网络,最近邻模型。
- 非监督模型:仅根据输入数据对数据进行分组和解释;数据驱动(聚类);聚类(Clustering),降维(Dimensionality Reduction),异常检测(Anomaly Detection)
- 强化学习:算法学会对环境做出反应;目标导向 (学习政策或最大化“奖励”);自适应动态规划,时间差分(TD)方法,q学习
监督学习划分
分类:如果输出变量是离散的(分类到特定的类别或类) 示例:根据动物的特征将其分类为物种;性能通常由分类的准确性/精确度来衡量。 回归:如果输出变量是连续的 示例:根据提供的参数预测房价;通常通过计算预测输出与目标之间的差异来衡量绩效。
神经网络
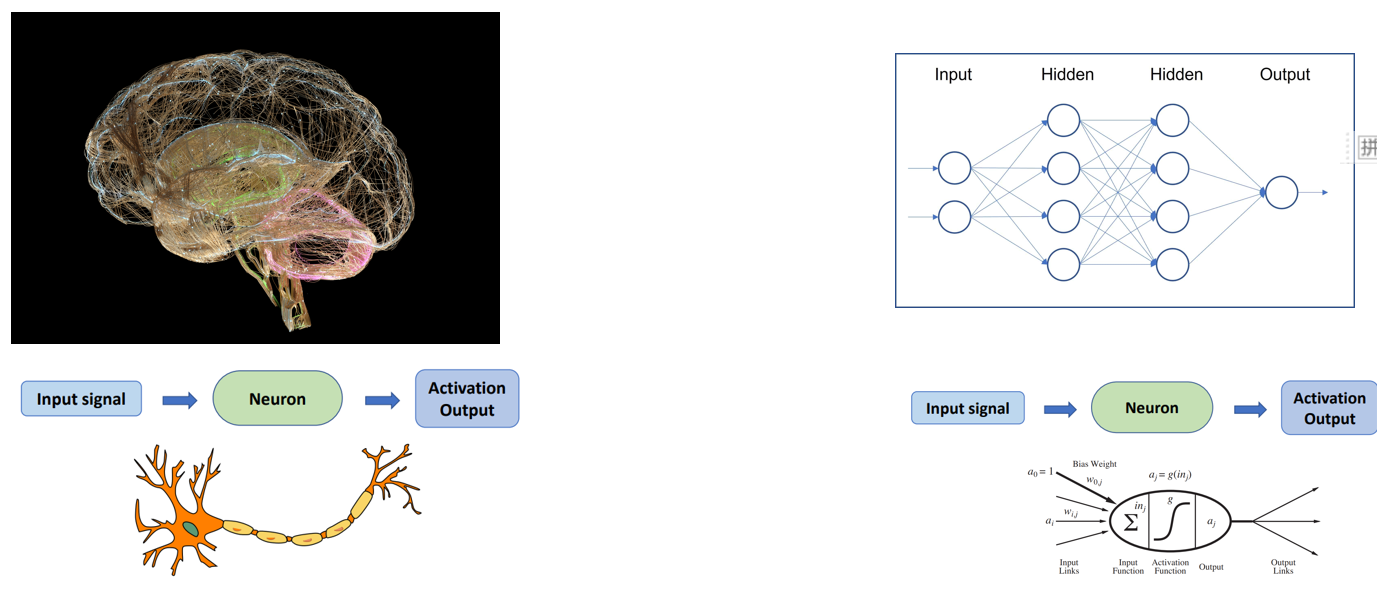
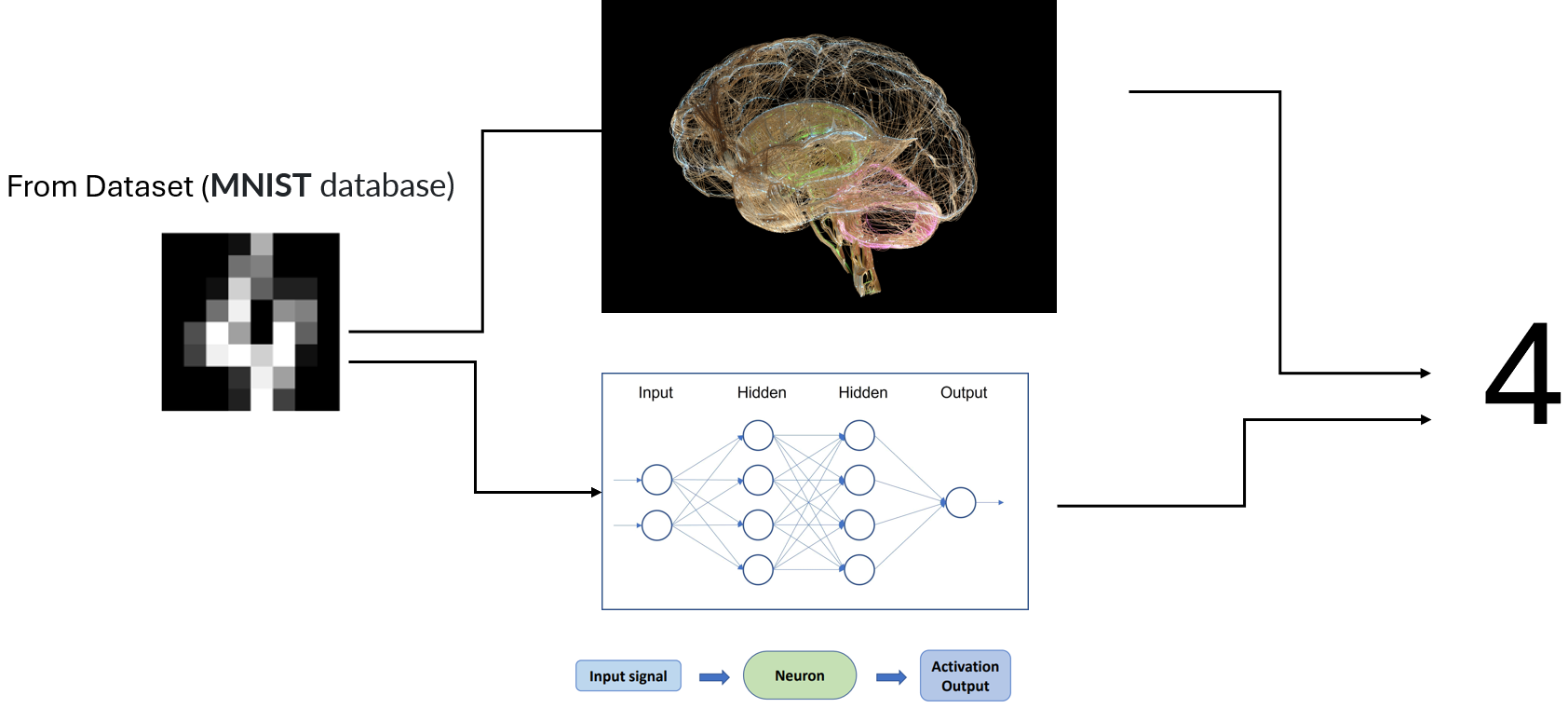 神经网络是受大脑启发的计算模型,旨在识别模式。关键思想:通过调整神经元之间的权重从数据中学习。
神经网络是受大脑启发的计算模型,旨在识别模式。关键思想:通过调整神经元之间的权重从数据中学习。
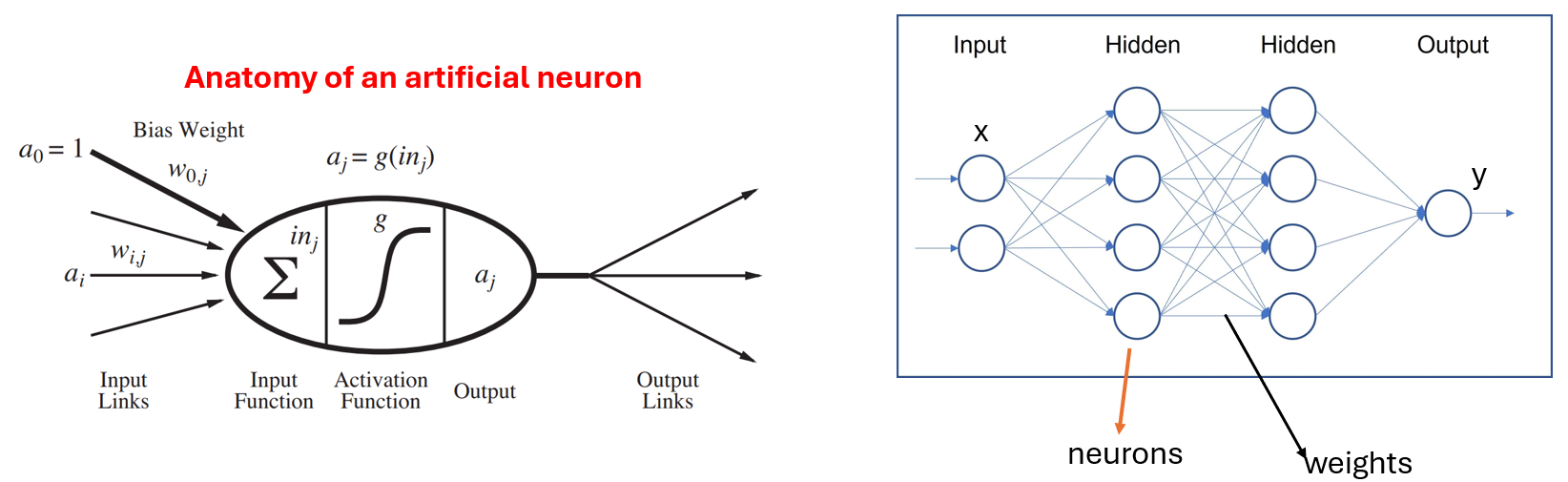 神经元/节点接收输入,执行计算,并通过激活函数传递结果。
层由输入层、一个或多个隐藏层和输出层组成。
神经元通过权重连接,在学习过程中进行调整。激活函数是应用于神经元输出的数学函数。
神经元/节点接收输入,执行计算,并通过激活函数传递结果。
层由输入层、一个或多个隐藏层和输出层组成。
神经元通过权重连接,在学习过程中进行调整。激活函数是应用于神经元输出的数学函数。
单层感知器
神经网络的最简单形式,仅由输入层和输出层组成。
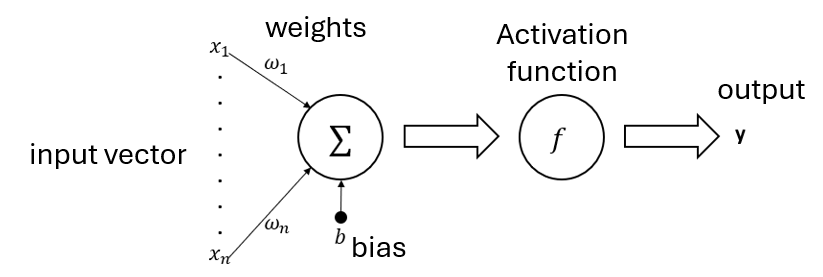 其中,X为输入向量,𝑤为权重,𝑏为偏置项,𝑓为激活函数,y而为输出。
公式如下:
其中,X为输入向量,𝑤为权重,𝑏为偏置项,𝑓为激活函数,y而为输出。
公式如下:
$$ y = f(\sum_{i=1}^{n} w_i \cdot x_i + b) $$
激活函数
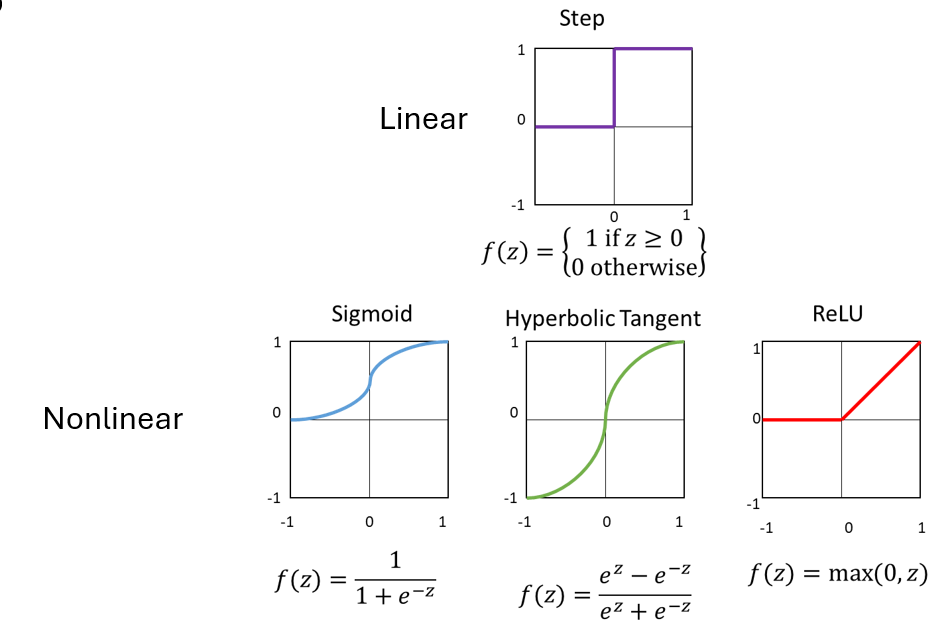 目的:引入非线性,允许网络学习复杂的模式。
目的:引入非线性,允许网络学习复杂的模式。
感知器学习的算法
感知器学习算法(Perceptron Learning Algorithm,PLA)是感知器模型的基本算法。 它通过调整权重来学习。 它的步骤如下:
- 初始化权重为0。 2. 对于每个训练样本,计算输出值。 3. 如果输出值与目标值不同,则更新权重。 4. 重复步骤2和3直到所有样本都被正确分类或达到最大迭代次数。
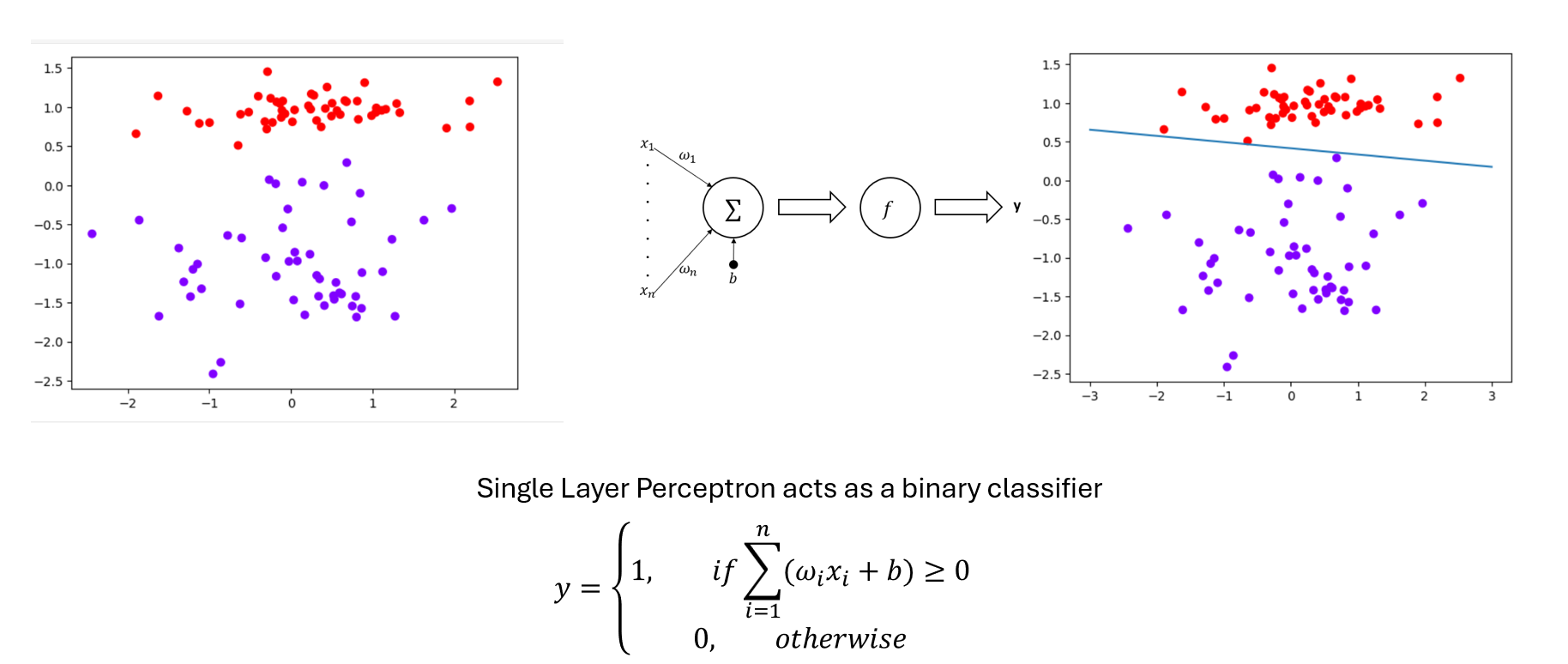
感知器的局限性
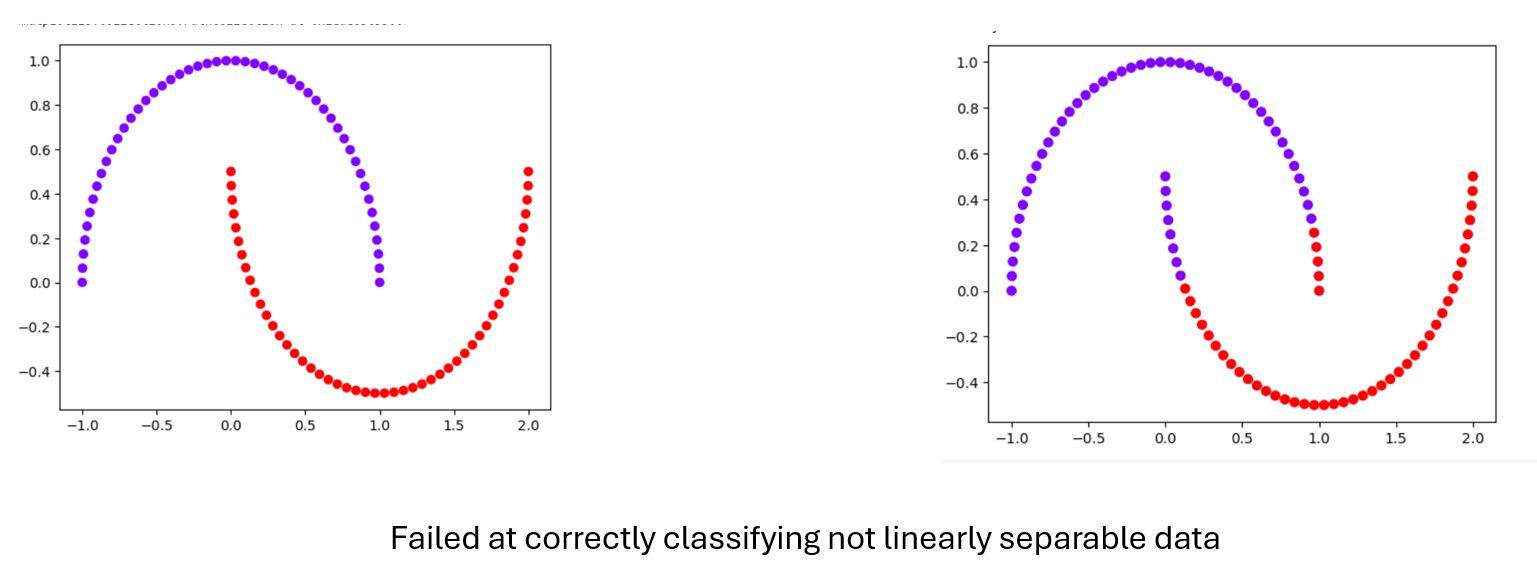
感知机只能解决线性可分问题(即,类可以被直线或超平面分开的问题)。
当数据是线性可分时,感知器学习规则保证收敛,但对于非线性可分数据,感知器学习规则可能不收敛。
为了处理更复杂的问题,我们需要超越SLP而转向多层感知器。
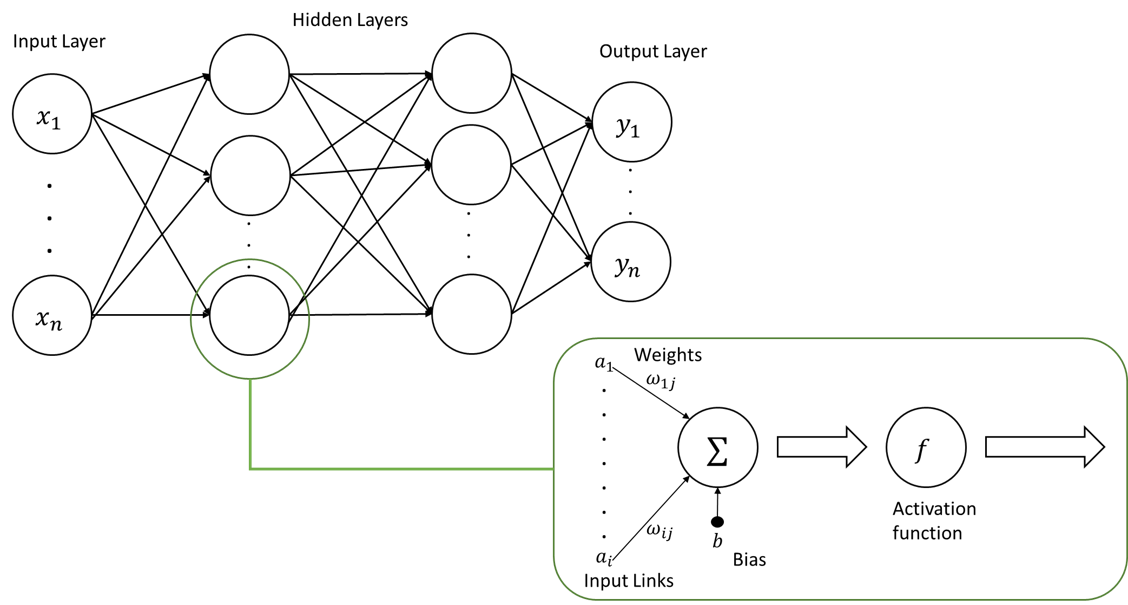
多层感知器
在输入层和输出层之间有一个或多个隐藏层的更高级的神经网络。网络表现出高度的连通性,每个隐藏节点形成一个线性分离边界; 将所有隐藏节点组合形成一个输出节点,有效地创建一个分段的线性(或非线性)分离边界。
激活函数的选择
选择激活函数时,需要考虑以下几点:
- 非线性:激活函数应引入非线性,以便神经网络能够学习复杂的模式和特征。
- 可微性:激活函数应是可微的,以便使用梯度下降法进行优化。
- 计算效率:激活函数应计算效率高,以便在训练和推理过程中快速计算。
常见的激活函数包括:
Sigmoid:输出范围在(0, 1)之间,常用于二分类问题,但容易导致梯度消失问题。
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
Tanh:输出范围在(-1, 1)之间,相比Sigmoid更适合处理零均值数据,但仍可能导致梯度消失。
$$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$
ReLU (Rectified Linear Unit):输出为输入的正部分,计算简单且有效,但可能导致“神经元死亡”问题。
$$\text{ReLU}(x) = \max(0, x)$$
Leaky ReLU:ReLU的变种,允许小的负梯度,缓解“神经元死亡”问题。
$$\text{Leaky ReLU}(x) = \begin{cases} x & \text{if } x > 0 \ \alpha x & \text{if } x \leq 0 \end{cases}$$
Softmax:常用于多分类问题,将输出转换为概率分布。
$$\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}$$
选择激活函数时,通常需要根据具体问题和数据进行实验和调整。
多层感知器的算法
多层感知器的算法与单层感知器的算法类似,但需要考虑多层的权重更新规则。 它的步骤如下: 1. 初始化权重为0。 2. 对于每个训练样本,计算输出值。 3. 如果输出值与目标值不同,则更新权重。 4. 重复步骤2和3直到所有样本都被正确分类或达到最大迭代次数。
损失函数
损失函数:测量预测输出和实际标签之间的差异。-应该仔细选择,因为它既反映了神经网络输出的性质,也反映了它试图解决的问题。常见的损失函数:均方误差(MSE)用于回归,交叉熵用于分类。
神经网络总结
- MLP可以解决更复杂的非线性问题
- 有很多参数需要调整(隐藏层的数量,神经元等)
- 更多的层和神经元增加了计算复杂性
- MLP比slp更强大,更通用。mlp可用于多类分类和回归
SLP:简单的架构,仅限于线性可分问题。 MLP:可以解决更复杂的非线性问题
- 训练:使用反向传播等技术来优化权重。许多参数需要调整(隐藏层的数量,神经元等)
- 应用:神经网络可以用于各种领域,如图像分类,语音识别和文本分析。