线性回归的定义
线性回归是一种统计方法,用于在一个因变量和一个或多个自变量之间建立关系模型。其基本思想是通过拟合一条直线,使得数据点到该直线的距离之和最小,从而找到最佳拟合的线性关系。线性回归模型可以表示为:
$$ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n + \epsilon $$
其中,$ y $ 是因变量,$ x_1, x_2, \ldots, x_n $ 是自变量,$ \beta_0, \beta_1, \ldots, \beta_n $ 是回归系数,$ \epsilon $ 是误差项。
高维线性回归示例
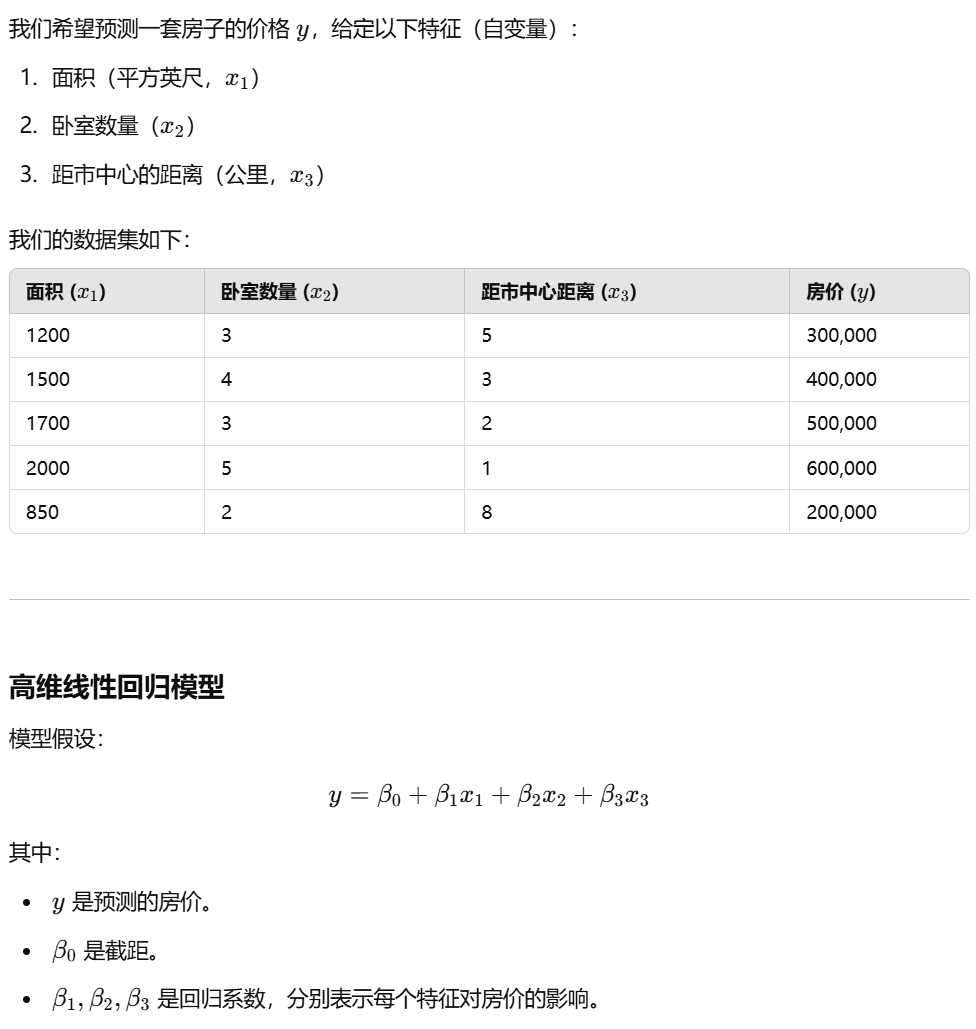


假设我们有一个包含多个特征的数据集,我们希望通过高维线性回归来预测目标变量。以下是一个简单的例子:
import numpy as np
# 数据输入
# X 是特征矩阵,y 是目标向量
X = np.array([
[1, 1200, 3, 5], # 1 表示截距项
[1, 1500, 4, 3],
[1, 1700, 3, 2],
[1, 2000, 5, 1],
[1, 850, 2, 8]
])
y = np.array([300000, 400000, 500000, 600000, 200000])
# 计算 (X^T X)^(-1) X^T y
# 公式: beta = (X^T X)^(-1) X^T y
X_transpose = X.T
beta = np.linalg.inv(X_transpose @ X) @ X_transpose @ y
# 输出回归系数
print("回归系数 (beta):")
print(beta)
# 模型公式
print("\n模型公式:")
print(f"y = {beta[0]:.2f} + {beta[1]:.2f} * x1 + {beta[2]:.2f} * x2 + {beta[3]:.2f} * x3")
# 预测新数据
# 假设房子特征: 面积 1800 平方英尺, 卧室 4, 距市中心 3 公里
new_data = np.array([1, 1800, 4, 3]) # 注意加 1 对应截距项
predicted_price = new_data @ beta
print("\n预测房价:")
print(f"面积: 1800 平方英尺, 卧室: 4, 距市中心: 3 公里")
print(f"预测房价: ${predicted_price:.2f}")
梯度下降
当无法获得解析解时(如非线性模型或数据过于复杂),使用梯度下降法(Gradient Descent)是一种有效的数值优化方法。
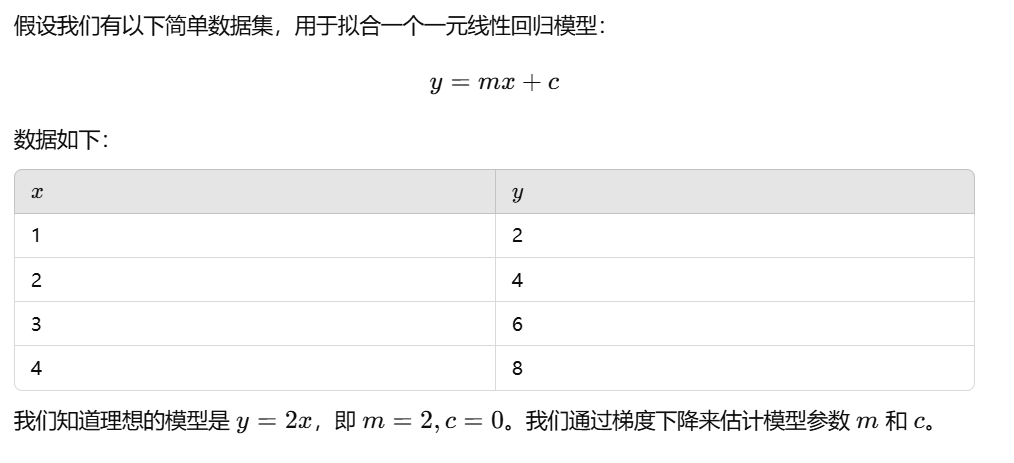

import numpy as np
# 数据集
X = np.array([1, 2, 3, 4])
y = np.array([2, 4, 6, 8])
# 初始化参数
m, c = 0.0, 0.0 # 初始斜率和截距
learning_rate = 0.1 # 学习率
epochs = 1000 # 最大迭代次数
n = len(X)
# 梯度下降
for epoch in range(epochs):
# 预测值
y_pred = m * X + c
# 计算梯度
dm = -(2/n) * np.sum(X * (y - y_pred))
dc = -(2/n) * np.sum(y - y_pred)
# 更新参数
m -= learning_rate * dm
c -= learning_rate * dc
# 打印损失值(可选)
if epoch % 100 == 0:
loss = np.mean((y - y_pred) ** 2)
print(f"Epoch {epoch}: Loss = {loss:.4f}, m = {m:.4f}, c = {c:.4f}")
# 输出结果
print("\n最终结果:")
print(f"斜率 m: {m:.4f}")
print(f"截距 c: {c:.4f}")
梯度下降的关键点:
- 初始参数:m=0.0,c=0.0。模型完全不准确,误差较大。
- 逐步优化:每次迭代中,通过梯度下降公式,调整 m 和 c,让模型误差逐渐减小。
- 收敛:经过多次迭代,m 和 c 会接近实际值 m=2,c=0。
Epoch 0: Loss = 30.0000, m = 4.5000, c = 1.2000
Epoch 100: Loss = 0.0025, m = 1.9979, c = 0.0045
Epoch 200: Loss = 0.0000, m = 2.0000, c = 0.0000
最终结果:
斜率 m: 2.0000
截距 c: 0.0000